솔직히 기존까지 알고리즘 공부를 많이 해봤지만, 매번 기억에 남는 것은 하나도 없었다. 이 책의 제목과 표지만을 봤을 때 조금 달랐던 점은, 자바 또는 파이썬 코드 위주의 알고리즘 문제 풀이 서적과 다르게 어떻게든 이해시키려고 노력한다는 것이었다. 정의를 먼저 소개하고 활용법을 제시하기보다 문제 상황을 먼저 던진 다음, 이런 경우라면 어떻게 해결할 수 있겠는가? 라는 질문으로부터 출발하는 방식이 매우 마음에 들었다.

여기서 간단히 내가 회사에서 하는 업무를 소개하자면, Elasticsearch/OpenSearch와 같은 검색엔진 클러스터를 구축 및 관리하는 역할로 파면 팔수록 Computer Science적 지식을 필요로 하는 분야다. (깊게 들어가면 사실 그렇지 않은 분야가 있겠냐만은..) 아래 두 가지 특징을 살펴보면, 왜 자료구조와 알고리즘 지식이 뒷받침되어야 하는지 알 수 있다.

1. Heap

• C/C++의 Pointer의 개념이 없는 Java에도 여전히 객체의 참조는 관리해야 하므로, 객체 저장소인 heap 관리 역할의 OOP(ordinary object pointers)라는 자료구조가 존재한다. 32bit 시스템(ILP32)에서 OOP는 최대 4GB(= 2^32bit), 64bit에서는 18.5EB(= 2^64bit)까지 쓸 수 있다. 64bit에서는 포인터의 크기가 4 -> 8바이트로 두 배가 되어 포인터 자체가 차지하는 메모리와 캐시 공간이 많이 늘어난다. 물리적(한 서버에 EB 단위까지 메모리가 증설되는 것은 사실상 불가능)인 관점에서나 논리적(Heap 크기가 크면 미사용 객체의 참조를 해제하는 GC 과정에서 STW가 너무 길어짐)인 관점에서 많은 64bit 가상머신에서는 포인터 압축을 통해 32bit의 OOP를 이용하고 있다. 

• 물론 (32bit OOP의) 4GB짜리 Heap은 운영 환경의 워크로드에는 역부족이다. 때문에 객체 그 자체를 참조하는 것이 아닌, 객체의 offset을 참조하는 Compressed OOP 방식을 사용한다. 즉, 64bit 기반 JVM이 OOP는 32bit 기반으로 유지하면서, 4GB 이상의 Heap 영역을 갖도록 만든 것이다. 만약 32GB 이상 Heap을 설정하면 JVM은 자동으로 다시 Native OOP(64비트 참조) 로 변경됩니다. CPU는 메모리에서 데이터를 읽을 때 버스를 통해 특정 크기의 덩어리(block)로 로드한다. 이때 일반적인 Cache Line이 8개의 8바이트 크기로 이루어지므로, JVM 역시 객체를 8바이트 단위로 정렬한다. (객체 주소가 8바이트 정렬되어 있으므로, offset은 항상 8의 배수) 32비트 정수로 표현 가능한 최대 값은 2^32−1입니다. 여기서 offset에 8을 곱하면 최대 32GB(= 2^32×8)까지 표현 가능하다.

2. HNSW (Hierarchical Navigable Small World)

 대부분의 VectorDB들은 모두 임베딩 벡터를 저장함에 있어, KNN의 엄청난 계산량을 감당하기보다는 Approximate하게 근접 이웃을 찾아내고 있는데, Graph 이론 기반의 HNSW 알고리즘이 대표적이다. (HNSW 구현체로는 Faiss가 있음)

• 전통적인 자료구조(kd-tree나 ball-tree) 기반의 방법은 저차원에서는 우수한 성능을 보이지만, 차원의 저주(curse of dimensionality)로 인해 임베딩 벡터와 같이 고차원 데이터를 다룰 때는 성능이 급격히 저하된다. 이에 반해 HNSW(Hierarchical Navigable Small World) 알고리즘은 그래프 이론에서 착안한 ‘Small World’ 네트워크의 특성을 적극 활용하여, 데이터 간의 연결 관계를 다층적인 그래프로 모델링함으로써 탐색의 효율성과 정확도를 동시에 확보한다.

• HNSW 알고리즘은 여러 층(layer)으로 구성된 그래프 구조를 사용한다. 가장 낮은 0층은 모든 데이터를 포함하는 완전한 그래프로 구성되며, 상위 층으로 올라갈수록 점점 적은 노드들이 포함된다. 상위 층들은 근접성에 따라 샘플링된 대표 노드들의 집합으로 구성되며, 전체 데이터셋의 대표성을 띠면서도 탐색 시 초기 진입점 역할을 수행한다. 탐색이 시작되면, 초기에는 상위 층의 노드들 사이에서 대상 벡터와의 거리를 측정하며, 가장 가까운 노드를 찾아낸다. 이후 그 노드를 시작점으로 하위 층에서의 탐색을 진행하는데, 이때 각 노드는 자신의 인접 노드들과 연결되어 있어, 점진적으로 탐색 범위를 좁혀가며 최종적으로 근사 최근접 이웃을 찾게 된다.

* 간단하게 말해보는 감상평

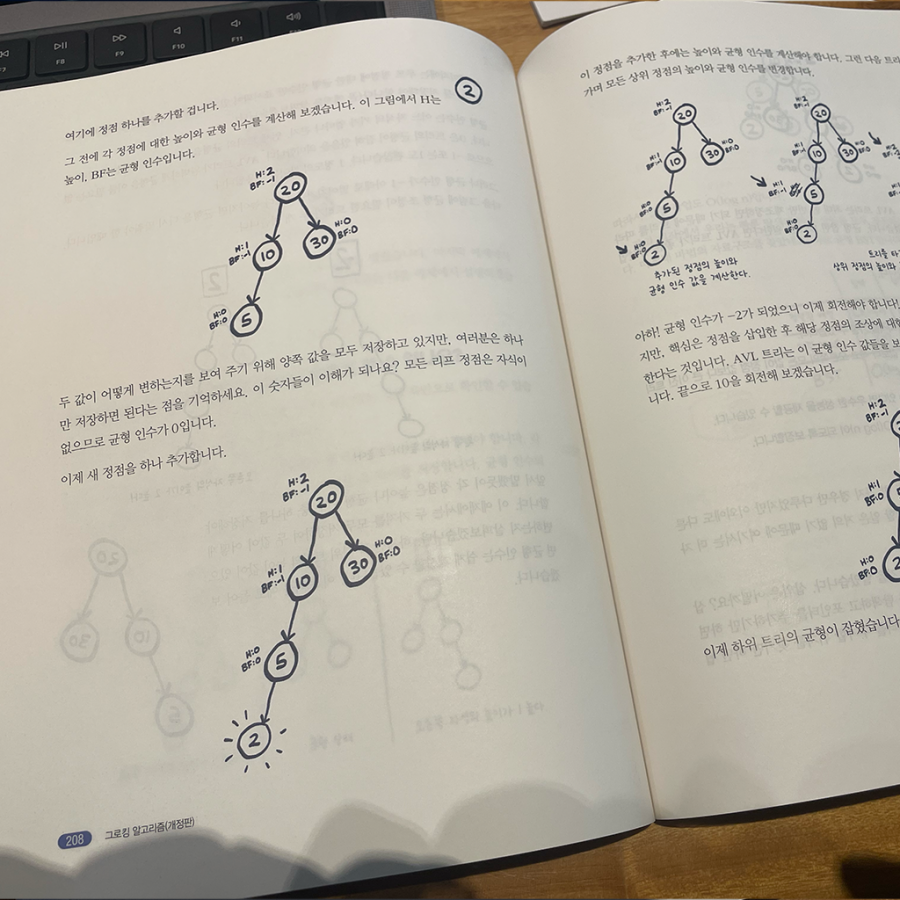
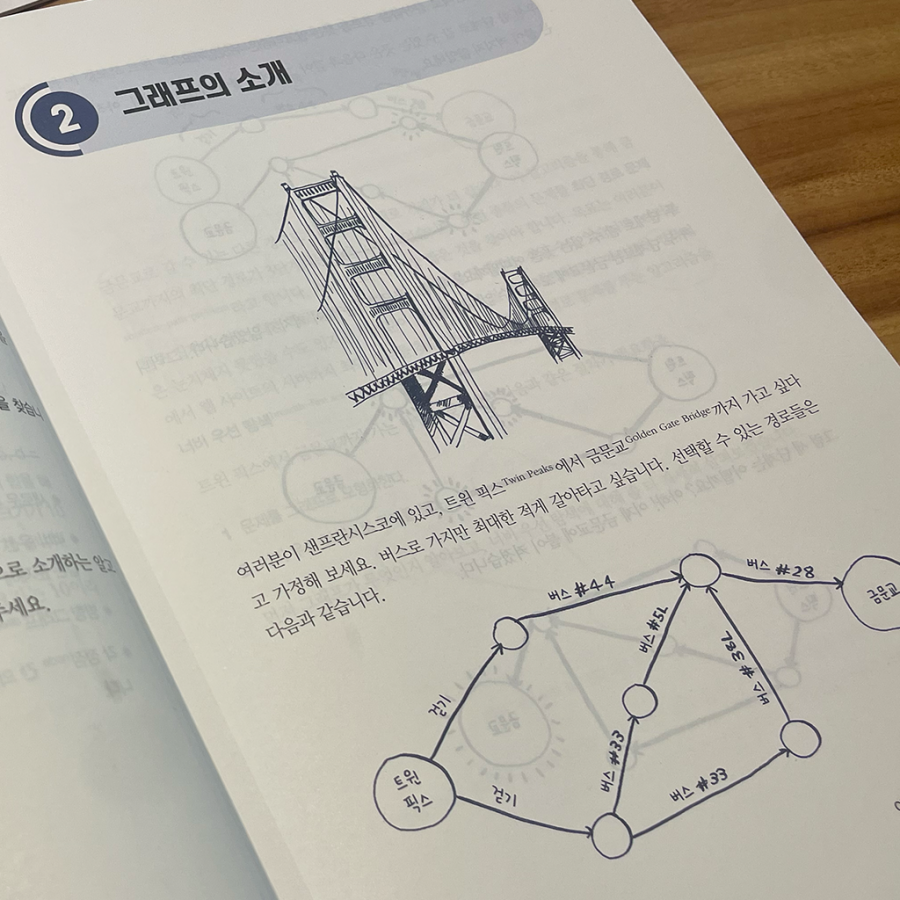
• 자료구조의 단순 설명 나열이 아닌, 하나의 자료구조(ex. 그래프)에서 파생된 또 다른 자료구조(ex. 트리), 그리고 그 자료구조를 활용한 알고리즘(ex. 허프만 코딩)을 이해시키는게 기가 막히다.
• 가장 기본적인 배열과 연결리스트의 장단점을 알려주면서, 원하는 성능을 제공하지 못하면 트리를 사용해야 하는 이유에 대해서도 친절하게 소개한다.
• 알고리즘 코딩 스터디를 하기 전, 개념 잡는데 꼭 참고하면 좋을 책이다.

그림으로 개념을 이해하는 그로킹 알고리즘 (개정판)

   아디티야바르가바 지음

   김도형 옮김

이번 책은 "그로킹 알고리즘" 이라는 알고리즘 입문서 입니다.

알고리즘 책으로써 2017년 초판이 발행된 이후 꾸준히 사랑받고 있는 책 입니다.

이유는 ... 쉽게 풀어서 설명하고 있기 때문이겠죠.

초판 발행 이후 개정판이 출간 되었습니다.

알고리즘 입문서라고 하지만 프로그래밍 하면서 기본적으로 사용되는 알고리즘 부터 좀 더 확장된 알고리즘도 일부 다루고 있습니다.

[ 대상 독자 ]

알고리즘에 관심있는 모두 .... 를 대상으로 한다고 생각됩니다.

[ 책    구성  ]

이 책은 총 13개의 장으로 구성되어 있습니다.

책의 시작은 정형화 되어 있지는 않네요. 시작하기에 앞서 섹션이 있는 장이 있고 아닌 장이 있어요.

중요한 부분은 아니지만, 시작하기에 앞서 섹션에서 해당 장에서 학습 하고자 하는 목표가 무엇인지를 그리고 미리 알면 좋은 것에 대해서 정리 되어 있습니다.

 1장, 알고리즘의 소개

       01. 시작하기에 앞서

       02. 이진 탐색

       03. 빅오 표기법

 2장, 선택 정렬

       01. 메모리가 작동하는 방식

       02. 배열과 연결 리스트

       03. 선택 정렬

       04. 예제 코드

 3장, 재귀

       01. 시작하기에 앞서

       02. 재귀

       03. 기본 단계와 재귀 단계

       04. 스택

 4장, 퀵 정렬

       01. 시작하기에 앞서

       02. 분할 정복

       03. 퀵 정렬

       04. 빅오 표기법 복습

 5장, 해시 테이블

       01. 해시 함수의 소개

       02. 해시 함수

       03. 해시 테이블을 사용하는 예

       04. 충돌

       05. 성능

 6장, 너비 우선 탐색

       01. 시작하기에 앞서

       02. 그래프의 소개

       03. 그래프란 무엇인가 ?

       04. 너비 우선 탐색

       05. 그래프의 구현

       06, 알고리즘의 구현

 7장, 트리

       01. 시작하기에 앞서

       02. 루트가 있는 트리

       03. 깊이 우선 탐색

       04. 이진 트리

       05. 허프만 코딩

 8장, 균형 트리

       01. 시작하기에 앞서

       02. 균형 잡기

       03. 작은 트리가 더 빠르다

       04. AVL 트리: 균형 트리의 일정

       05. 스플레이 트리

       06. B 트리

 9장, 다익스트라 알고리즘

       01. 너비 우선 탐색 vs 다익스트라 알고리즘

       02. 다익스트라 알고리즘

       03. 용어 설명

       04. 다익스트라 알고르즘을 사용한 물물 교환

       05. 간선의 가중치가 음수인 경우

       06. 구현

10장, 탐욕 알고리즘

       01. 수업 시간표 짜기 문제

       02. 배낭 채우기 문제

       03. 집합 커버링 문제

11장, 동적 프로그래밍

       01. 배낭 채우기 문제

       02. 자주 하는 질문

       03. 최장 공통 부분 문자열

12장, KNN 알고리즘

       01. 오렌지와 자몽 분류하기

       02. 추천 시스템 만들기

       03. 회귀 분석

       04. 머신러닝의 소개

       05. 머신러닝 모델 훈련의 개요

13장, 더 공부해야 할 것

       01. 선형 회귀

       02. 역 인덱스

       03. 퓨리에 변환

       04. 병렬 알고리즘

       05. 맵-리듀스

       06. 블룸 필터와 하이퍼로그로그

       07. HTTPS와 디피-헬만 키 교환

       08. 지역 민감 해싱

       09. 최소 힙과 우선순위 큐

       10. 선형 프로그래밍

부록,

   A, AVL 트리의 성능

   B, NP-난해 문제

이 책은 알고리즘에 대해 좀 더 쉽게 다가갈 수 있게 하기위해 일상적인 예제와 많은 그림들을 적절하게 사용하고 있습니다.

내용 설명 중 필요에 따라 " TIP" 박스를 두어 알면 좋을 용어나 찾아 보면 좋을 내용들 그리고 꼭 알아야 할 부분들에 대해서 알려 주고 있습니다. 말 그대로 TIP 입니다. 상세한 부분을 다루지는 않습니다.

각 장의 마지막에는 어떠한 부분들을 담고 있었는지의 각 장에서 배운 항목들에 대한 한줄 요약과 연습문제가 있어서 각 장에서 배운 것에 대해서 한번 생각 해볼 수 있도록 정리 되어 있습니다.

아, 연습문제에 대한 풀이는 부록에 포함되어 있습니다.

연습문제 중에서 문제 해결에 대한 대한 풀이는 문제에 따라서 풀이가 여러가지가 있을 수 있기에 부록의 풀이는 정답이다 라기 보다 이러한 형태로 접근할 수 있구나로 이해하고 다른 방법들은 없는지도 생각해보면 좋을 것 같습니다.

[ 결 론 ]

알고리즘 관련된 책은 엄청 많은 것 같습니다.

대부분이 딱딱한 학습서일 것이라 생각되는데, 이 책은 많은 내용을 담기 보다 기본에 충실하며, 그리고 좀 더 알고리즘과 자료 구조에 대해 친근하게 다가갈 수 있도록 저자의 노력이 보이는 책 입니다.

자칫 잘못하면 예를 들어 설명하는 부분들이 더 어렵게 받아 들일 수 도 있는데, 이 책은 각각의 내용에 맞게 적절하게 잘 표현되어 있는 것 같습니다.

알고리즘이 처음 이라면 이 책을 학습한 후 다음 책으로 넘어가면 좋을 것 같습니다.

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."
 

IT 세계에서 현실 세계의 복잡한 문제를 해결하기 위해 프로그래밍을 사용하고 프로그래밍이라는 과정을 거쳐 하나의 프로그램이 완성된다. 그런데 프로그램은 시간과 공간의 제약을 받을 수 밖에 없는 태생적 한계를 갖고 있기 때문에 보다 효율적으로 자원을 사용하기 위한 노력이 수반돼야 한다. 즉 최초에 프로그램을 작성할 때부터 효율성을 고려한 알고리즘 전략을 세워야 하고 이를 통해 비로소 시간과 공간의 제약을 극복할 수 있는 기반이 마련된다. 일련의 문제 해결을 위한 절차인 알고리즘은 비단 프로그래밍에 국한되지 않지만, 프로그래밍 세계에서 어느 정도 정형화되고 보편화된 다양한 기법이 존재하고 있으며 이는 우리보다 앞서 여러가지 문제를 해결한 선구자들과 거인의 어깨 위에 올라선 거장들의 노력 덕분에 고안되었고 지금껏 우리는 그 혜택을 톡톡히 누릴 수 있게 된 셈이다. 그런데 알고리즘을 학습하는 것이 결코 쉽지 않은데, 그 이유는 특정 알고리즘을 이해하기 위해 필히 선행되어야 하는 배경지식과 그에 따른 표현에 있어 다양한 수식이 동반되기 때문이다. 그래서 알고리즘 학습을 시작하는 이들이 시작하기도 전에 지레 겁을 먹거나, 학습 도중 포기하는 경우을 종종 목격하게 된다. 그렇다면 보다 쉽게 알고리즘을 학습할 수 있는 방법은 없을까? 오늘 소개하는 서적이 바로 그 물음에 대한 답이 되어 줄 수 있으리라 생각한다.

여타 서적과 마찬가지로 이 책은 빅오 표기법을 위시하여 기본적인 알고리즘 학습 토픽으로 자주 사용되는 정렬, 트리, 재귀, 탐색 등 다양한 알고리즘 기법에 대한 설명이 저자의 독특한 표현 방식과 풍부한 그림을 통해 전달된다. 난해하고 복잡한 수식 대신 간결하고 직관적인 도해로써 쉽지 않은 알고리즘도 어느 순간 이해의 영역에 다가서게 된다. 물론 모든 알고리즘을 그림으로써 온전히 표현할 수 있다면 더 할 나위 없겠지만 적어도 특정 알고리즘이 어떻게 코드로 구현되는지에 대한 이해도 반드시 필요하기 때문에 본 서적에서는 그러한 사항을 충족하기 위해 파이썬 코드로 설명이 확장된다. 따라서 파이썬에 대한 기본적인 이해가 선행되어 있다면 보다 더 나은 학습으로 이어질 수 있겠지만 그렇지 않더라도 핵심을 이해하는 데 크게 문제되지는 않는다. 중요한 건 알고리즘이 어떻게 동작하며, 어떤 논리 구조를 갖추고 있는지 파악하는 것이며 그림을 통해 그러한 일련의 흐름을 따라갈 수 있다면 그것만으로도 충분하다고 볼 수 있겠다. 마지막 챕터에서는 추가적으로 공부해야 하는 영역을 제시하면서 다양한 기법의 알고리즘에 대한 소개도 놓치지 않고 있다. 

이 책은 복잡한 수식 없이도 실세계에서 다양하게 사용되는 알고리즘에 대해 누구나 쉽게 다가갈 수 있도록 도와 주며 명쾌하고 탁월한 설명으로 알고리즘 학습의 정도를 제시한다. 알고리즘의 늪에 빠져 허우적대는 모든 이들에게 이 책을 통해 다시금 알고리즘 학습을 재개하기를 권고하며, 처음 알고리즘 학습을 시작하는 초심자에게도 이 서적과 함께 진정한 알고리즘의 세계로 온전히 진입할 수 있기를 추천한다. 비록 이 책 한 권으로 알고리즘 학습을 완성할 수 없지만 적어도 알고리즘의 기초를 쌓고 더 나아가 심화된 학습을 이어 갈 수 있는 지적 근육이 충분히 단련되리라 생각한다. 알고리즘 학습을 망설이고 있다면, 지금 바로 이 서적과 함께 학습을 시작해 보면 어떨까?
 

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."

이번에 제가 선택했던 책은 그로킹 알고리즘이라는 책인데요.

제가 해당 책을 읽고 싶다는 생각을 하게 된 계기는 코딩 테스트를 위해서가 아닌 알고리즘 자체를 학습해보고 다양한 상황에서 겪게 되는 문제를 해결할 때 좋은 해결 방안을 도출하는 경험을 해보고 싶었기 때문이에요. 그리고 해당 책은 제 니즈에 맞게 내용이 구성되어 있는 것 같아 읽어보게 되었습니다.

책은 초반부에는 알고리즘이 무엇인지에 대해서 설명하고 빅오 표기법을 설명하는 시간을 갖습니다. 빅오 표기법은 대부분의 사람들에게 익숙하겠지만 왜 중요한지에 대해서 조금 더 자세하게 설명해주고 있는 느낌이었어요.

이후에는 배열, 연결리스트, 재귀와 같은 알고리즘의 기초가 되는 내용에 대해서 학습을 시작하고 나머지 부분에서는 다양한 알고리즘들을 소개하고 있어요. 이 알고리즘들은 코테에서 많이 언급되는 내용에 덧붙여서 더 공부하면 좋을만한 내용들도 많이 포함하고 있어요.

가장 인상적이라고 느꼈던 부분은 책 표지에 있는 "그림으로 개념을 이해하는"이라는 표현에 맞게 알고리즘에 대한 모든 설명이 그림과 같이 실생활의 예시를 들어서 설명하고 있다는 점이에요. 알고리즘을 공부할 때 어렵게 느껴지는 부분중에 하나는 "실제로 이런 알고리즘을 어디에 사용하지?"라는 부분도 빠질 수 없다고 생각하는데 해당 고민에 대한 내용을 해소시켜주는 것 같아서 좋았어요.

먼저 알고리즘에 대한 개념 이해를 돕고, 이후에 해당 알고리즘이 적용되는 문제를 어떻게 해결할 수 있을지 차근차근 설명하는 방식으로 진행되는 것이 어려운 개념을 공부할 때도 도움이 많이 되었던 것 같아요.

그리고 각 챕터의 마지막에는 제대로 학습했는지를 확인할 수 있는 연습문제가 있어요. 공부를 할 때 가장 중요한 것은 제대로 공부를 했는지 내가 판단할 수 있어야 한다고 생각하는데요. 확인할 수 있는 방법으로는 인출을 하는 방법이 제일 좋다고 생각해요. 저도 이론적인 내용을 공부할 때는 책을 보지 않고 스스로 학습한 지식을 모두 꺼내보는 연습을 하는데요. 자연스럽게 챕터의 마지막에 연습문제를 풀면서 비슷한 과정을 경험할 수 있어서 이 부분도 좋았던 것 같아요.

해당 책은 코딩테스트를 위한 알고리즘을 공부하는 목적으로도 읽을 수 있지만 저처럼 알고리즘 자체를 평소에 어렵게 느끼시거나, 혹은 개념을 위주로 공부하고 싶은 니즈가 있으신 분들에게 꼭 추천드리고 싶은 책중에 하나입니다.

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."

이 책은 수학적 엄밀함보다 직관적으로 이해를 도와주는 알고리즘 입문서입니다.

특히 복잡한 개념이 대부분 시각적으로 표현해서 쉽게 이해할 수 있었습니다.

기본적인 자료구조와 대표 알고리즘을 귀여운 그림과 함께 이해할 수 있어서 재미있게 읽었습니다. 코드는 파이썬으로 간단하게 제시되고 복잡할 수 있는 실행 과정은 시각화되어서 직관적으로 이해할 수 있었습니다.

알고리즘을 공부할 때 그림으로 정리하는 것이 큰 도움이 됐는데 이 책도 그렇게 미리 준비해 둔 느낌이 듭니다.

+ 기본 개념이 익숙한 분께는 쉬울 것 같습니다.

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."

복잡한 알고리즘 개념을 친근한 그림과 직관적인 설명으로 쉽게 풀어낸 보석 같은 책입니다. 파이썬 예제를 사용하지만 개념 이해에 중점을 두고 있어 자바스크립트 개발자인 저도 큰 어려움 없이 학습할 수 있었습니다. 특히 이진 탐색, 해시 테이블, 동적 프로그래밍 부분은 프론트엔드 성능 최적화에 직접 적용할 수 있어 실무에 큰 도움이 되었습니다. 알고리즘을 처음 접하는 개발자부터 개념을 복습하려는 경험자까지 모두에게 강력 추천합니다!

“한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.”

 작년에 이미 알고리즘 책 한 권 봤는데, 왜 또 이걸 읽고 있는 거지? 사실 이유는 두 가지다. 첫 번째는 아무리 봐도 안 쓰니까 자꾸 잊어버려서 계속 봐야 한다는 것이고, 두 번째는 “그림으로 개념을 이해”한다는 표현에 꽂혀서다. 그래서 이 책을 보자마자 아이들에게 이런 책이 있다고 뀌띔했다. 그림으로 쉽게 이해할 수 있다면, 아이들에게 한 번 읽어보라 싶었다. 수업 중에 정보가 있고, 그러면 어쩔 수 없이 알고리즘은 배울 테니, 도움이 되지 않을까, 하는 막연한 생각이 들어서다.

 그런데 첫 번째 이유는 나름 타당해서 문제가 없었는데, 두 번째는 문제가 생겼다. 중학교 정보 서적에서 알고리즘을 봤는데, 굳이 이런 전문도서의, 그래도 입문서격인 책이, 사실 필요없는 수준이라는 점이다. 섣부른 판단일지도 모르겠지만, 적어도 교과서 내용에서는 이 정도 수준까지 요구하지는 않을 거라는 생각이 들었다. 정보가 재밌고, 코딩이 재밌고, 그래서 주어진 문제를 해결하는 게 재밌어서 알고리즘을 제대로 공부해보자 하지 않는다면, 이 정도 난이도의 책도 아이들에겐 마냥 어려운 책일 수밖에 없겠구나 싶었다. 그래서 두 번째는 포기했다.

 여기서 문제, 작년에 본 책을 다시 꺼내 슬슬 넘겨보며 읽어봤다. 그 책도 충분히 잘 만든 책이라 생각했는데, 이 책과는 결이 다른 게 눈에 보였다. 지난 책도 충분히 “기술”적으로 접근해서 잘 설명해주고 있다 생각했는데, 아무래도 그건 전산인의 눈으로 봐서 그랬을 수도 있겠다는 생각이 들었다. 저자는 프로그래밍을 취미로 시작했다가 알고리즘을 책으로 접했다가 방대한 양에 포기했다가 훌륭한 교수를 만나 그 기본 개념을 알아가기 시작했다고 말한다. 그러면서 본인이 “시각적으로 학습하는 것을 선호하고, 그림으로 설명하는 것에 익숙”하다고 말한다. 이게 이 책의 정체성을 설명하는 중요한 표현이라 생각한다.

 처음 책을 펼칠 때 나의 기대는 만화책같은 느낌이지 않을까 하는 생각이었다. 곧 그건 잘못된 생각이라는 걸 알게 됐지만, 적절한 그림 표현과 문장들은 해당 내용을 전달하는 데 있어 매우 효과적이고, 심지어 코드와 해당 코드 상황에서의 그림 표현은 이해를 도울 뿐만 아니라, 머릿속에 콱콱 박아넣는 듯한 인상을 줬다. 괜히 “아마존 프로그래밍 언어 분야 베스트셀러”가 아니었다.

 알고리즘의 소개를 통해 배경을 알려주고, 선택 정렬과 재귀, 퀵 정렬을 거쳐 해시 테이블과 너비 우선 탐색, 트리, 균형 트리로, 다익스트라 알고리즘, 탐욕 알고리즘, 그리고 동적 프로그래밍과 KNN 알고리즘으로 나아간 다음, 더 공부해야 할 것에서 최근 핫한 내용들과 연결되는 알고리즘들을 추가로 언급한다.

 내용이 빈약한 것 아닌가? 하는 생각이 든다면, 그건 과욕이다. 사실 학술적으로 접근하면 한 장 한 장 그 분량이 대단해서 입문서가 아니라 전공서적이 되어버릴 테니까. 이만큼이나 다루는데도 핵심만 쏙쏙 짚어주면서도 설명이 쉽고 간결하다. 주요한 지점에서는 그림과 결합하여 이해하기 쉽게 전개한다. 그래서 막힘이 없기에 술술 잘 읽히는 느낌도 있다.

 한 장 한 장 끝날 때마다 배운 내용을 요약하고, 연습문제를 낸다. 그런데 그 문제가 꽤 현실적이라 문제를 위한 문제로 느껴지지 않는 것도 대단하다면 대단하다. 중간 중간 나온 팁도 매우 유용하다.

 처음 읽었을 때 꽤나 신선하게 다가온 설명 중 하나는 “메모리가 작동하는 방식”이었다. 메모리를 서랍에 비유하니 재밌었다.

 허프만 코딩도 들어는 봤고, 쓰기도 했지만, 사실 동작 원리를 이해하고 쓰진 않았는데, 이 책에서 설명하는 내용을 보고 이제야 기초적인 이해를 한 것 같다. 사실 그냥 쓰기만 할 거라면 몰라도 되지만, 프로그래밍에 응용할 거라면, 알아두는 게 무척 도움이 될 만하다.

 실제로 그래프, 특히 트리 개념은 알게 모르게 엄청나게 사용하고 있기에, 이해하는 게 절대적으로 필요하다. 그걸 이렇게 쉽게 설명하니 대단하다. 다익스트라 알고리즘은 매번 볼 때마다 어려웠는데, 이 책에서 너무 잘 설명해줘서 무척 도움이 됐다.

 이 책에서 앞서 설명한 알고리즘으로 그 다음 알고리즘을 구성하거나 설명하는 식의 패턴이 해당 내용을 이해하는 데 큰 도움을 줬다. 보통은 그런 연결성을 유추하거나 지나가는 말 중에 하나로 취급할 텐데, 여기서는 앞에 알고리즘이 여기서 어떤 영향을 주고 왜 이렇게 되었는지를 아주 요긴하게 쓰고 알려 준다. 때로는 비교를 통해 왜 이게 되고 이게 안 되는지도 알려 준다. 이렇게 해주니 이해가 쉬울 수밖에. 과거 강의 시간에 배웠던 방식과는 달라서 너무 좋다. 그 때 이렇게 배웠다면 얼마나 좋았을까… 뭐 내가 게으른 탓이지만.

 거듭 설명하지만, 입문서다. 이걸로 해당 알고리즘을 다 알았다고 하면 안 된다. 적어도 그 알고리즘을 깊이 이해하기 전, 기본 개념을 잡는 데에는 매우 유용한 책임을 주지해야 한다. 그렇다고는 해도 너무 가볍게 볼 필요도 없다. 이 책을 써서 프로그래밍을 한다고 해도 문제 될 건 없어 보인다. 이해하고 짜는 것도 이해 안 하고 대충 써서 짜는 것은 엄연히 다르다. 그 결과가 다르다. 결국 같은 결과를 얻더라도 O(log n)으로 나올지 O(n!)으로 나올지는 선택의 문제다. 올바른 선택을 위해서는 이 책을 추천한다. 후회하지 않을 거다.

코딩테스트를 공부하며 

알고리즘 개념이 잘 생각나지 않을 때 이 책을 보며 공부하였습니다.

덕분에 효율적으로 준비할 수 있었습니다.

“한빛미디어 서평단 ＜나는리뷰어다＞ 활동을 위해서 책을 협찬 받아 작성된 서평입니다.”

알고리즘을 배울 때 가장 어려운 점은 개념을 머릿속에서 이미지로 떠올리기 어렵다는 것이다. 이 책은 시각적인 접근 방식을 활용해, 복잡한 알고리즘을 쉽게 이해하도록 돕는다.

책을 읽으면서 크게 세 가지 부분이 유용했다.

1️⃣ 그림으로 배우는 알고리즘 개념

2️⃣ 코딩 없이 사고하는 연습문제

3️⃣ 각 장에서 배운 내용을 정리하는 리뷰 섹션

2. 장점

✅ 직관적인 그림 설명

트리, 정렬, 탐색 알고리즘 등을 그림으로 설명하여 개념을 빠르게 이해할 수 있다.

특히, 퀵소트(Quick Sort)와 최대공약수(GCD) 알고리즘은 그림 덕분에 확실히 정리되었다.

✅ 연습문제로 사고 확장

단순한 코드 예제가 아니라, 탐색 알고리즘을 활용한 문제 해결 방식을 고민하게 만든다.

예를 들어, 트럭에 짐을 최적화해서 싣는 방법, 여행 경로를 최적화하는 문제 등을 탐색 알고리즘과 연결하여 사고하도록 유도한다.

✅ 장별 요약으로 개념 복습

책을 읽으면서 중요한 내용을 놓치지 않도록 각 장의 핵심 내용을 정리해준다.

예를 들어, 이진 탐색이 O(log n)인 이유를 한 번 더 되짚어볼 수 있다.

3. 아쉬운 점

입문자에게는 매우 적합하지만, 심화된 알고리즘 문제 풀이가 부족하다.

시간 복잡도 분석과 최적화 기법을 좀 더 깊이 다루었으면 좋았을 것 같다.

알고리즘을 실무에 적용하는 부분이 보강되었으면 더 좋았을 듯.

4. 추천 대상

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."

먼저 그로킹이라는 생소한 단어가 눈에 띄어 검색을 해보니, 로버트 하인라인의 SF 소설 '낯선 땅 이방인(Stranger in a Strange Land)'에서 처음 사용된 단어라고 하고 '깊이 이해하고 완전히 터득한다'는 의미를 가지고 있다고 한다. 이 의미로 이 책의 제목인 [그로킹 알고리즘]을 유추해 보면 알고리즘을 깊이 이해하고 완전히 터득하자라는 의미인 것 같다.

먼저 이 책에서 다루고자 하는 알고리즘에 대해 알아보자.

저자는 알고리즘의 일반적인 의미인 '어떤 일을 하기 위한 명령의 집합체'라는 프로그램을 구성하는 모든 코드를 지칭하는 알고리즘이 아닌 알고리즘을 보다 효율적으로 구성하기 위한 방법에 대해 다루고 있으며 이를 위해 여러 알고리즘의 장단점에 대해 배우게 된다고 한다.

하지만 알고리즘 공부가 쉽지만은 않을 것이다. 단순한 듯 보이는 개념조차 조금씩 알아가면 점점 어려워지고 수식은 낯설며, 코드만 봐서는 도무지 이해가 되지 않는 상황이 나에게 다가오게 되는데, 이를 이해하기 위해 빼곡하게 적힌 설명글을 읽고 이해한다는 건 쉽지 않을 것이다.

하지만 그 과정에 '다양한 도식과 그림을 활용하여 개념을 설명'한다면 좀 더 쉽게 되지 않을까. 예를 들어, 이 책의 첫번째로 설명하고 있는 [이진 탐색]을 설명하며, 1과 100 사이의 어떤 숫자를 찾는 과정을 설명하며, 단순히 "중간 값을 찾고, 크기에 따라 절반을 버린다"라는 설명글만 있지 않고, 숫자가 정렬된 리스트 위에서 특정 숫자를 찾아가는 과정을 단계별 그림으로 보여주면서 나의 머릿속에 [이진 탐색]이라는 개념이 자연스럽게 자리 잡게 한다.

이런 방식으로 어렵게 느껴질 수 있는 개념을 최대한 쉽게 설명한다. 선택 정렬, 재귀, 퀵 정렬, 너비 우선 탐색, 다익스트라 알고리즘 등 다양한 알고리즘이 등장하지만, 설명 방식이 직관적이라서 따라가기가 어렵지 않다. 코드 예제도 최소한으로 유지하면서 개념을 중심으로 설명하는 점이 인상적이었다.

그리고 이 책은 어떤 알고리즘을 설명하기에 앞서 독자 스스로 알고리즘을 생각해 보는 시간을 준다는 것이다. 그런 후, 문제를 풀어가는 여러가지 방법을 비교해 가면서 가장 좋은 방법을 찾아가는 과정을 설명하고 있어 다양한 방법을 능동적으로

익히게 되는 시간을 가지게 되는 것 같다.

그리고 이 책은 초보자뿐만 아니라 알고리즘을 다시 정리하고 싶은 사람에게도 좋은 책일 것 같다. 일단 기본적인 개념을 다루고 있지만, 단순히 개념을 나열하는 것이 아니라 문제 해결 방식과 사고 과정 자체를 다루기 때문에, 이미 알고리즘을 공부한 사람들에게도 좋은 복습 자료가 될 수 있을 것이라 생각된다.

​

결론적으로, 『그림으로 개념을 이해하는 그로킹 알고리즘』은 알고리즘을 처음 접하는 사람들에게 더없이 좋은 입문서라고 생각한다. 복잡한 개념을 단순한 그림과 설명으로 풀어내어, 알고리즘을 보다 직관적으로 이해할 수 있도록 도와주고 있고, 문제 해결 과정을 스스로 생각해볼 수 있도록 유도하하는 과정을 거치면서 단순한 개념 암기가 아니라 사고력을 기를 수 있게 하고 있어, 알고리즘 공부가 어렵다고 느껴지는 분들이나 어디서부터 시작해야 할지 막막한 분들에게 이 책을 꼭 한 번 읽어보기를 추천한다.

​

한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬받아 작성된 서평입니다.

​

전업맘이 되기 전, 저는 프로그래머였는데요.

그럼에도 불구하고 저는 수포자이고, 알고리즘에 대한 이해가 거의 없는 편이라 알고리즘이라는 단어만 들어도

머리가 지끈거렸어요.

아이가 어느 정도 크면 재취업을 해야 할 것 같아 처음부터 시작하는 마음으로 알고리즘에 대해 공부해 보려고 그로킹 알고리즘을 선택해 읽어보게 되었어요.

저자는 이 책에서 단순히 알고리즘의 이론적인 부분만 설명하는 것이 아니라, 이를 실생활의 예시와 함께 비주얼 자료를 통해 풀어내고 있었는데요. 그래서 초보자도 쉽게 이해할 수 있었어요.

일반적인 알고리즘 책들은 복잡한 코드와 수학 공식으로 가득 차 있는 데 반해 이 책은 다양한 일러스트가 가득해서 알고리즘을 공부할 때 조금 더 쉽게 접근할 수 있을 것 같다는 생각이 들더라고요.

또 처음에는 간단한 예제와 개념으로 시작해 차근차근 난이도가 높아지는 방색이라 이러한 책의 구성도 마음에 들었어요.

이 책을 보면서 알고리즘을 배운다는 것은 프로그래밍을 넘어 문제를 해결하는 사고방식을 키우는 데도 도움이 된다는 걸 느꼈는데요. 저처럼 알고리즘이 어렵게 느껴지는 수포자라면 이 책으로 알고리즘 공부 시작해보시길 추천드려요!

목차.

1. 알고리즘의 소개

2. 선택 정렬

3. 재귀

4. 퀵 정렬

5. 해시 테이블

6. 너비 우선 탐색

7. 트리

8. 균형 트리

9. 다익스트라 알고리즘

10. 탐욕 알고리즘

11. 동적 프로그래밍

12. KNN 알고리즘

13. 더 공부해야 할 것

저는 오늘 그림으로 개념을 이해하는 그로킹 알고리즘 책에 대해서 서평을 해보려고 합니다. 이 책은 알고리즘을 배우고자 하는 사람들에게 매우 유용한 자료로, 특히 그림을 통해 개념을 쉽게 이해할 수 있도록 돕는 점이 매력적입니다. 필자도 한참 알고리즘 학습을 하고 시험도 많이 봤는데요. 특히나 처음 입문하는 사람에게는 일러스트를 통해 쉽게 설명이 되어있어서 이해하기 쉽도록 되어있습니다.

그럼 본격적으로 책에 대해서 서평을 하도록 하겠습니다.

책 소개

그로킹 알고리즘은 알고리즘에 대한 기초 지식이 없는 사람도 쉽게 이해할 수 있도록 구성된 책입니다. 이 책의 특징은 바로 다양한 그림과 설명을 통해 복잡한 개념을 설명한다는 점입니다. 표지를 보면 아기자기한 동물들이 그려져 있는데요, 이처럼 시각적으로 매력적인 일러스트가 많은 도움을 줍니다.

처음에는 이진 탐색, 선택 정렬, 재귀, 퀵 정렬 같은 기본적인 알고리즘 개념을 배우면서 문제 해결의 기초를 다진다. 이후에는 해시 테이블, 너비 우선 탐색(BFS), 깊이 우선 탐색(DFS), 균형 트리 등을 배우면서 데이터 구조와 탐색 기법을 심도 있게 익힌다.

여기서 끝이 아니라, 탐욕 알고리즘(Greedy Algorithm)과 동적 프로그래밍(DP)까지 다루면서 최적화된 문제 해결 방법을 학습할 수 있다. 탐욕 알고리즘은 빠른 해결 방법을 찾을 때 유용하고, 동적 프로그래밍은 더 복잡한 최적화 문제를 해결하는 데 필수적인 기법이다.

이뿐만 아니라, 다익스트라 알고리즘을 통해 가중 그래프에서의 최단 경로 탐색을 배우고, KNN 알고리즘과 머신러닝 개념까지 접할 수 있다는 점도 매력적이다.

일반적인 알고리즘 책에서는 다루지 않는 선형 회귀, 병렬 알고리즘, 맵-리듀스, HTTPS, 블룸 필터, 최소 힙 같은 고급 개념까지 다뤄서, 실무에서 활용할 수 있는 배경 지식을 넓힐 수 있습니다.

단순히 코딩 테스트를 대비하는 용도로 끝나는 게 아니라, 실제 개발에서 성능 최적화, 보안, 데이터 처리까지 고려할 수 있도록 도와주는 책이라 더 가치가 있습니다.

책의 특징 특/장점

이 책의 가장 큰 특징은 복잡한 수학이나 프로그래밍 지식 없이도 누구나 쉽게 이해할 수 있도록 구성되어 있다는 점입니다. 알고리즘을 배우는 데 있어 많은 사람들이 느끼는 진입 장벽을 낮추기 위해, 직관적인 삽화와 예시를 사용하고 있습니다.

이 책은 여러 가지 알고리즘을 단순하고 명확하게 설명하여, 독자가 쉽게 그 개념을 이해할 수 있도록 해줍니다. 예를 들어, 이진 탐색(Binary Search)을 도서관에서 책을 찾는 과정으로 비교해 설명하는데, 이런 비유가 직관적으로 이해하는 데 큰 도움이 되었습니다. 특히 알고리즘에 대한 부담이 적어지니까, 처음 접하는 사람들에게 아주 적합하다고 생각됩니다.

주요 내용 및 구성

책은 여러 장으로 나뉘어 있으며, 각 장마다 다양한 알고리즘을 다루고 있어요. 예를 들어, 이진 탐색(Binary Search) 같은 기본적인 알고리즘부터 시작해, 정렬 알고리즘, 그래프 이론 등 다양한 주제를 다루고 있어요. 각 장은 그림과 함께 설명이 되어 있어, 독자가 쉽게 따라갈 수 있도록 돕고 있어요.

그림과 예시의 중요성

그림을 통한 이해는 특히 어린 독자나 알고리즘에 대한 배경 지식이 없는 사람들에게 큰 도움이 돼요. 복잡한 개념을 시각적으로 표현함으로써, 독자는 더 쉽게 이해하고 기억할 수 있어요. 이 책은 그런 점에서 매우 효과적이에요.

실제 사용 사례

실제로 이 책을 읽으면서 제가 느낀 점은, 일상생활에도 적용할 수 있는 알고리즘들이 많다는 것이었어요. 예를 들어, 친구와의 약속을 잡을 때 최적의 장소를 찾는 과정에서도 알고리즘이 활용되는 것을 느낄 수 있었어요. 이런 점들이 독자에게 실질적인 도움이 되어 주는 것 같아요.

마무리 및 추천

결론적으로, 그림으로 개념을 이해하는 그로킹 알고리즘은 알고리즘을 배우고 싶지만 방법이 막막한 분들에게 정말 강력하게 추천하고 싶습니다. 쉽게 접근할 수 있는 내용과 재미있는 일러스트가 가득하니, 한번 읽어보시길 강력히 권장합니다.

저는 이 책을 통해 알고리즘에 대한 이해가 한층 깊어졌다고 생각합니다. 그림과 함께하는 학습은 정말 재미있고, 어렵게 느껴졌던 알고리즘이 한결 친숙하게 다가왔어요. 알고리즘을 배우고 싶지만 두려워하는 분들에게 강력히 추천하고 싶습니다!

한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.​

​

이 책을 선택한 이유는 최근 개발을 하면서 알고리즘 필요성이 많이 느껴져서이다.

주니어 개발자 당시 알고리즘 책들을 많이 봤지만 그동안 잘 안 쓰다 보니 잊어버린 게 대부분이고 그때그때 찾아보기 바빴다.

그래서 목표는 개념 정리!!

그로킹이란?

일단 난 저 단어의 의미를 몰랐다 ㅋㅋ

그래서 찾아보니 groking, "완전히 이해하다" 라는 뜻이었다.

한국말 번역하면 완전히 이해하는 알고리즘 이랄까?

난이도

책에서는 알고리즘에 대한 개념을 그림으로 설명해 주는데 사실 프로그래머가 아니더라도 읽기엔 부담이 없다.​

기본적으로 프로그래밍 능력보다는 수학적인 능력을 요구하고 그 수준이 높지 않기에 이해하는데 어렵지는 않다.

우리가 학생 때 배운 정렬이나 탐색 알고리즘이 대표적인 예고 프로그래머들이 실무에서 자주 쓰는 트리 알고리즘과 같이 일반인들? 은 모르는 알고리즘도 나온다.

​

구성

각 챕터에서는 먼저 생소할 수 있는 알고리즘 용어에 대해 설명해 준다.

이후 알고리즘에 대한 기본적인 개념 설명과 알고리즘을 이해할 수 있게 단계별로 차근차근 일러스트로 설명해 준다.

여기서 나도 읽으면서 알았는데 기본적인 흐름을 파이썬으로 설명해 주는데 나도 잘 모르는 언어이지만 워낙 기본적으로만 나와있어 언어를 몰라도 된다.

그리고 마지막엔 해당 챕터에서 배운 알고리즘 문제와 해답이 나온다.

​

마치며

아마 주니어 개발자나 코딩 테스트 준비를 하는 취준생들이 찾아볼 거 같다.

대표적인 알고리즘 사이트인 백준 알고리즘 사이트에 가면 여기서 배운 개념을 바탕으로 코딩 문제를 풀 수 있으므로 좀 더 내 것으로 만들려는 분들에게는 추천한다.

“한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.”

시작에 앞서
이 책은 코드가 (거의) 없는 알고리즘 책이다. (코드는 파이썬이다.)
드디어 올해 졸업반이다. 올해의 목표는 칼취업이다. 따라서 6대 과목을 전부 맛보고 조금씩 코테 감각을 끌어올리는 느낌으로 지내고 있다. 자료구조 알고리즘은 무시무시한 과목이자 코테에 필요한 덕목인지라 이 책을 고르게 됐다. 알고리즘 책을 사서 본 적이 없다보니 한 번 읽어보면서 이론적 맥락과 구현 방법을 전체적으로 톺아보고 싶었다.

책의 이름은 (그림으로 개념을 이해하는) 그로킹 알고리즘
이 책의 제목은 이러하다. 그림이 진짜 많고 귀엽다. 그림은 러프한 스케치처럼 보여서 알고리즘 문제를 풀 때 종이나 패드에 끄적거린 느낌이라 단순하고 직관적이다. (그림은 못그리려고 하지만 은근히 잘 그렸다.)
그로킹이라는 말의 뜻도 찾아봤다. 어떤 소설책에 나온 용어로, 이 책에서 화성인들은 무언가에 대한 심오한 이해 또는 깊고 직관적인 파악을 묘사할 때 이 단어를 사용했다. 무언가를 '파악'한다는 것은 그것과 하나가 되거나 그 본질을 완전히 이해할 정도로 철저하게 이해한다는 뜻이라고 한다.

알고리즘이 필요한 이유를 상상력과 함께 설명해준다
알고리즘을 설명할 때, '상상해보죠', '가정해봅시다'와 같은 말로 시작한다. 코드는 진짜 아주 짧게 주는 느낌이다. 그런 의미에서 파이썬을 몰라도 충분히 읽을 수 있다. 파이썬은 굉장히 직관적인 언어라 수도코드 느낌으로 읽어도 되지 않을까 싶기도 하다.
동화책, 그림책을 읽듯이 자연스럽게 상상하면서 읽다보면 복잡도, 정렬, 배열, 기타 등등에 대해서 다룰 수 있기에 정말 좋다.

코딩을 처음 시작할 때 백준을 풀기 위해서 처음 도서관에서 잡고 읽었던 책이 코드 없는 알고리즘과 데이터 구조인데, 이런 계열의 책은 정말 쉽고 잘 알려준다. 간만에 공부를 하기 좋다.

다루는 알고리즘
크게 두 파트로 볼 수 있는데, 메인은 코딩테스트에서 자주 보는 알고리즘이며, 머신러닝에서 들어본 것 같은 알고리즘과 추가로 공부해보면 좋을 알고리즘을 서브로 다룬다.

메인이 되는 코딩테스트에서 자주보는 알고리즘은
코테 준비하면서 자주 마주하는 대중적인 알고리즘을 다룬다. 정렬, DP, 그리디, BFS, 다익스트라 등등을 다룬다. 나같은 비전공자, 자료구조 알고리즘을 공부하지 못한 저학년 학생들은 일단 이런 책을 읽으면서 개념을 잡는게 정말 좋다고 생각했다. 코드가 별로 없는게 큰 장점이다.

읽고 얻은 것
아무래도 소마 합격 이후에는 코딩테스트 준비 자체를 안하다보니 코테 감각이 떨어진 것을 느껴서 방학동안 실버 수준이지만 문제를 종종 풀었다. 학기 중엔 골드1이 되버린 백준 계정을 플래5로 올릴 계획인데, 그 것에 큰 도움이 될 것 같다.
나는 방학 중에는 자바스크립트로 코테 준비를 해보려는 만용을 부렸다. 큐, 힙을 클래스로 직접 구현해야하는 고통을 겪어보니 파이썬이 최고다. 파이썬은 심지어 콤비네이션도 함수가 잘 빠져있다...
그래서 이 책을 기반으로 다시 파이썬 코드를 읽어보면서 감각을 조금 찾는 기분이 들었다. 너무 좋다.

올해 2학기가 지나면 졸업이고 면접을 볼텐데, 만약 (그럴 일은 없겠지만...?) 다익스트라 알고리즘을 설명해보세요. 같은 것을 물어본다면 지난달의 나는 코드로 구현은 할줄 알아도 어떻게 설명할지 답답했을 것 같은데, 이젠 될 것 같다. 글과 그림이 많다는 점도 이해하고 설명하는 방식도 밴치마킹할 수 있기에 면접 준비에도 내 기준에선 도움이 되는 책 같다.

한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.

알고리즘은 프로그래밍에서 빼놓을 수 없는 영역이다. 방대한 자료를 분석하고 요구사항에 맞는 해법을 내놓는데 최적의 해결방안을 내놓는데 필요한 것이 바로 알고리즘이다. 최적의 해결방안을 내놓는다는 것은 단순히 요구사항의 수행여부 뿐만이 아니라 실행 속도와 자원의 효율성으로 성능 개선을 한다는 의미도 있다. 오늘날 AI, 빅데이터같은 복잡하고 방대한 자료들 속에서 의미있는 결과를 도출하기 위해 알고리즘은 과거보다 더 중요해졌다.

오늘 소개할 책은 컴퓨팅으로 해결할 수 있는 문제들을 알고리즘으로 어떻게 최적화 하는지 알려준다. 앞서 말했듯 알고리즘은 최적의 해결방안을 위해 효율성을 따지는 기술이다. 단순히 무차별 대입이나 순차반복을 해도 주어진 요구사항을 해결하는데 아무런 문제가 없지만, 자료가 방대해진다면 처리하는데 걸리는 시간과 메모리 공간의 낭비는 증가할 것이다.

알고리즘-자료구조 책들은 대게 전공자들을 대상으로 하기 때문에 시간 복잡도를 나타내는 Big O 표현이나 공간 복잡도에 대해 바로 설명하는 경우가 많다. 그로킹 알고리즘이 친절한점은 처음부터 목적에만 집중하지 않고 문제를 해결하기 위한 여러 단계들을 제시하며 설명하고자 하는 바에 도달한다는 점이다. 가령 정렬을 설명하기 위해 가장 기본이 되는 선택정렬에서는 메모리와 배열이 어떻게 이뤄져있고 연결리스트와는 어떤 차이가 있는지 삽화로 자세히 설명한다. 정렬을 알기위해 필요한 모든 내용을 소개 후 선택정렬이 작동하는 방법을 설명한다.

그래서 그로킹 알고리즘은 코드보다는 도식이 담긴 삽화가 풍부하게 담겨있다. 또한 도식마다 그에 따른 설명도 같이 붙어있어 이론과 추론이 따로 설명된 책 보다 훨씬 편하게 볼 수 있었다. 그래서 알고리즘 뿐만 아니라 자료구조에 대해서도 처음 접하는 사람들이 본다면 이해를 금방 할 수 있을것이라 생각한다.

당연하게도 알고리즘에 대해서 이야기 하는 책이기 때문에 정렬, 이진 탐색, 그래프 탐색, 그리디 알고리즘, 동적 프로그래밍 알고리즘을 안다고 했을때 필요한 내용들은 모두 담겨있다. 또한 이러한 알고리즘을 이해하기 위해 필요한 배열, 연결 리스트, 스택, 해시 테이블, 트리, 그래프 같은 기초적인 자료구조 지식들을 같이 소개 한다. 또한 코딩 인터뷰에서 종종 분별력을 주기 위해 등장하는 동적 프로그래밍을 비롯해 역 인덱스, NP-hard 와 같은 내용들도 다루고 있어 허들을 넘어 알고리즘을 더 깊게 알게 되는데 도움이 됐다.

한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.

유튜브, 넥플릭스 등 개인 맞춤화 된 추천 시스템이 보편화 되면서 알고리즘이라는 용어가 흔하게 사용하고 있습니다. 프로그래밍에서 알고리즘은 분리될 수 없는 관계이자 점점 깊어지는 관계입니다. 컴퓨터를 전공하게 되면 자료구조부터 여러과목을 통해 알고리즘에 대한 개념을 익혀가게 됩니다.

그로킹 알고리즘은 알고리즘 문제 풀이를 위한 깊은 구현이나 응용을 이야기하는 책은 아닙니다. 알고리즘이라는 세계를 그림으로 소개해주는 책에 가깝습니다. 알고리즘에 있어 가장 기본인 시간 복잡도부터 NP-완전문제까지 다루고 있습니다. 깊은 내용까지 다루고 있지는 않지만 교양보다는 본격적인 알고리즘 서적에 가깝습니다.

일상의 상황, 기술 용어 그리고 일러스트가 알고리즘을 와닿게 이해시킵니다. 현실에서 만날법한 문제 상황으로 문제로 느끼지 않게 하면서 기술을 설명합니다. 사이 사이 끼어 있는 일러스트는 단계의 흐름을 통해 이해를 놓치지 않고 쫓아 갈 수 있게 도와주는 책입니다.

알고리즘 공부 시작을 하기엔 추천할 만한 책입니다. 자세한 코드 구현이 없어 아쉬울 수 있지만 기본적인 구현 형태를 보여주고 연습문제를 통해 응용 연습을 하게 해 충분히 기본 개념과 구현을 파이썬으로 익힐 만한 책입니다.

추천 대상: 알고리즘 입문, 알고리즘이 뭔지 궁금한 비전공자

개발자로 취업을 하려하면 알아야 하는 것중에 하나가 알고리즘이 아닐까? 코딩테스트 뿐만아니라 문제 해결을 하려고 원리를 파악하고 구조를 그리는 이 과정이 개발자에게는 중요한 능력인 것 같다 생각한다. 실질적으로 업무에 알고리즘을 사용하지 않는다 하더라도.

​

이 책의 예제 코드는 파이썬으로 이루어져있다. 역시 코딩테스트는 파이썬으로 해야하나보다.

​

그런 알고리즘에 대한 설명을 취합하여 책 하나로 만든게 "그로킹 알고리즘"인 것 같다. 알고리즘의 개념이 나한테는 어렵고 그래서 거리감이 느껴지는 부분이 있었는데, 차근차근 그림과 함께 예시를 들어 설명해주고 비유를 통해서 더 쉽게 설명하려고 하는 노력이 느껴진다.예제문제로 실습도 할 수 있으며, 예제에 대한 해설도 포함되어있다.

목차를 보면 코딩테스트 준비하면 알아야 한다는 모든 알고리즘이 들어가있는것을 알 수 있다.

개념에 대한 설명이 1개를 알려주고 그렇다면 이런 경우에는 어떨까?라는 흐름으로 차근차근 개념을 확장할 수 있게 해준다.

​

알고리즘을 처음 접하고, 강의나 영상을 봐도 이게 무슨소리인가 싶은 사람들이 차분하게 읽어나가면서 개념을 익히는데 아주 좋은 책이라고 생각한다. 나도 꾸준히 익숙해질때까지 여러번 읽어야지!

​

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."

한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.

왜 읽고 싶었나?

작년부터 꾸준히 알고리즘을 공부해왔지만, 코딩테스트에서는 시간 부족으로 문제를 다 풀지 못하거나, 어려운 문제를 혼자 해결하지 못하는 경우가 많았습니다. 이런 경험을 하면서 기초부터 다시 탄탄히 다져야겠다고 생각했습니다.

마침 <나는 리뷰어다 > 2월 리뷰 도서 목록에서 그로킹 알고리즘이 있었습니다. 온라인에서 종종 보던 책이었고, 추천 대상에 "알고리즘의 핵심 개념을 명확히 이해하고 싶은 개발자", "주니어와 시니어 모두에게 실질적인 도움을 주는 도서를 찾는 독자"라고 적혀 있었습니다. 저에게 필요한 책이라는 생각이 들어 신청했고, 운 좋게 리뷰 도서로 받아 읽게 되었습니다.

누구에게 추천하고 싶은가?

이 책을 읽으면서 주변에 추천해 주고 싶은 사람들을 떠올려 보았습니다. 아래와 같은 분들에게 추천하고 싶습니다.

• 전공 서적이 어려워 알고리즘 개념을 이해하기 힘든 대학생
• 기술 면접을 준비하며 알고리즘 문제를 공부하는 취준생
• 코딩 테스트 대비를 위해 기초를 다지고 싶은 취준생 및 이직 준비자
• 알고리즘 개념을 다시 정리하고 싶은 주니어 개발자

어떤 점이 좋았는가?

그로킹 알고리즘은 알고리즘 개념을 쉽게 이해할 수 있도록 직관적인 삽화와 쉬운 예시를 제공합니다. 예를 들어, 메모리를 서랍에 비유하고, 이를 시각적으로 보여주는 삽화와 함께 설명해 줍니다. 서랍 안에 물건을 정리하는 방식과 메모리에서 데이터를 저장·관리하는 개념을 연결해 설명하니, 개념을 직관적으로 이해하는 데 도움이 됐습니다. 쉬운 그림 예시로 어렵게 느껴지는 메모리, 너비 우선 탐색, 재귀 등의 개념을 부담 없이 가볍게 읽으면서 이해할 수 있다는 점이 좋았습니다.

또한, 각 장의 마지막에는 핵심 개념을 정리하는 요약이 포함되어 있어, 배운 내용을 한 번 더 되새길 수 있습니다. 이를 통해 저자가 강조하는 핵심 개념을 파악하고, 중요한 내용을 다시 정리하며 복습할 수 있었습니다.

그리고 각 챕터마다 연습문제가 포함되어 있어 방금 배운 내용을 복습할 수 있습니다. 이 연습문제는 코딩 테스트 문제처럼 복잡한 것이 아니라, 책에서 배운 개념을 제대로 이해했는지 확인하고 스스로 생각해볼 수 있도록 구성되어 있습니다. 덕분에 내가 어떤 부분을 제대로 이해했는지, 반대로 어떤 부분을 잘못 이해하고 있는지도 점검할 수 있었습니다.

한 줄로 표현하자면?

어렵게만 느껴지는 알고리즘을 그림으로 쉽게 풀어 이해할 수 있도록 돕는 책!

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."

보통의 알고리즘 책이 코드 구현과 최적화에만 집중하는 것과 달리, 『그로킹 알고리즘』은 실제로 언제 어떻게 알고리즘을 사용하는지에 초점을 맞춘 책입니다. 
개인적으로 알고리즘은 좋아하지만 관련 서적은 싫어했던 제가, 이 책의 직관적인 설명과 삽화에 완전히 매료되었습니다. 
코드는 간단한 파이썬 예제로 최소화하고, 대신 종이접기로 log(n)을 설명하는 등 재미있는 비유가 가득합니다. 
KNN이나 선형회귀 같은 머신러닝 기초 알고리즘도 다루고 있어 더욱 흥미롭게 읽었습니다. 
자료구조나 알고리즘을 처음 배우는 분들이 이 책으로 시작했다면 좋았을 것 같다는 생각이 들 정도로, 정말 추천하고 싶은 책입니다.

자세한 리뷰는 https://sonim1.com/ko/blog/review-grokking-algorithms-2nd-edition

한빛미디어 서평단 <나는 리뷰어다> 활동을 위해 책을 협찬 받아 작성된 서평입니다.

그로킹 알고리즘 책을 봐보자 

책 소개

한빛미디어에서 ‘나는 리뷰어다’ 서평단으로 선정되어 이 책을 받게 되었다. 두 권 중 랜덤으로 한 권이 올 예정이었는데, 내가 가장 원했던 그로킹 알고리즘을 받게 되어 기대가 컸다.

서점에서 제공하는 책 소개를 보면, 이 책은 복잡한 알고리즘 개념을 직관적으로 이해할 수 있도록 돕는 책이라고 나와 있다.

TMI
알고리즘은 개발자라면 중견 기업이나 서비스 기업으로 이직할 때 필수적으로 공부해야 하는 주제다. 나는 회사 지원할 때 알고리즘에 자신이 없어서 아예 코딩 테스트가 없는 회사들 위주로 지원했다. 하지만 경력 이직을 생각하면 결국 알고리즘을 공부해야 할 시기가 온다는 걸 깨달았다.

그런데 알고리즘은 입문하기가 쉽지 않다. 내 머리는 수학적으로 잘 안 돌아가는 것 같고, 이걸 제대로 공부하려면 오래 걸릴 것 같아서 부담스러웠다. 더군다나 알고리즘 책은 보통 너무 두꺼워서 시작하기도 전에 질려버리기 일쑤다. 그런데 이 책은 그런 부담을 줄여줄 수 있을 것 같아 기대되었다.

목차 요약

이 책은 알고리즘의 기초부터 고급 개념까지 단계적으로 설명하며, 각 장에서 개념을 배우고 연습문제를 통해 실습할 수 있도록 구성되어 있다.

단순히 기초적인 알고리즘 개념만 다루는 게 아니라, 실전에서 활용할 수 있는 다양한 문제 해결 방법까지 폭넓게 다룬다.

처음에는 이진 탐색, 선택 정렬, 재귀, 퀵 정렬 같은 기본적인 알고리즘 개념을 배우면서 문제 해결의 기초를 다진다. 이후에는 해시 테이블, 너비 우선 탐색(BFS), 깊이 우선 탐색(DFS), 균형 트리 등을 배우면서 데이터 구조와 탐색 기법을 심도 있게 익힌다.

여기서 끝이 아니라, **탐욕 알고리즘(Greedy Algorithm)**과 **동적 프로그래밍(DP)**까지 다루면서 최적화된 문제 해결 방법을 학습할 수 있다. 탐욕 알고리즘은 빠른 해결 방법을 찾을 때 유용하고, 동적 프로그래밍은 더 복잡한 최적화 문제를 해결하는 데 필수적인 기법이다.

또한 다익스트라 알고리즘을 통해 가중 그래프에서의 최단 경로 탐색을 배우고, KNN 알고리즘과 머신러닝 개념까지 접할 수 있다는 점도 매력적이다.

일반적인 알고리즘 책에서는 다루지 않는 선형 회귀, 병렬 알고리즘, 맵-리듀스, HTTPS, 블룸 필터, 최소 힙 같은 고급 개념까지 다뤄서, 실무에서 활용할 수 있는 배경 지식을 넓힐 수 있다.

단순히 코딩 테스트를 대비하는 용도로 끝나는 게 아니라, 실제 개발에서 성능 최적화, 보안, 데이터 처리까지 고려할 수 있도록 도와주는 책이라 더 가치가 있다.

전체적인 특징

• 기초 개념부터 실전 알고리즘까지 단계적으로 학습 가능
• 재귀, 정렬, 탐색, 그래프, 해시 테이블 등 핵심 알고리즘을 다룸
• 탐욕 알고리즘, 동적 프로그래밍, 머신러닝 등 실무와 연결되는 개념까지 포함
• 연습문제를 제공하여 실습하며 이해도를 높일 수 있음

장점

책을 아직 다 읽지는 않았지만, 앞부분을 읽어보면서 느낀 장점들을 정리해봤다. 알고리즘을 처음 접하는 사람들도 부담 없이 읽을 수 있도록 구성되어 있어서 입문자에게 특히 좋은 책이라고 생각된다.

1) 그림이 이해를 돕는다

책을 읽으면서 가장 좋았던 점 중 하나는 설명과 함께 제공되는 그림들이다. 알고리즘을 처음 배울 때는 개념이 머릿속에 쉽게 정리되지 않는 경우가 많은데, 단순한 텍스트 설명이 아니라 그림과 함께 설명해주니 훨씬 직관적으로 이해할 수 있었다.

2) 실생활과 연결된 예시 제공

이론적인 개념을 설명하는 것에서 끝나는 게 아니라, 일상 속 사례와 연결해서 설명해주기 때문에 이해가 쉬웠다. 예를 들어, 그래프 탐색을 설명할 때 지도에서 최단 경로를 찾는 개념과 연결해 설명해주는 식이다. 덕분에 "이 알고리즘이 실제로 어디에 쓰이는지" 감이 잘 왔다.

3) 부담스럽지 않은 분량

알고리즘 책이라고 하면 두꺼운 이론서가 먼저 떠오르는데, 이 책은 400페이지가 넘지 않아서 부담스럽지 않게 읽을 수 있었다. 입문서로 보기 좋은 두께라서 처음부터 끝까지 읽기에 부담이 적고, 중간중간 필요한 부분만 골라 읽기에도 좋을 것 같다.

4) 연습문제를 통해 개념을 다시 점검할 수 있음

각 챕터 끝에 연습문제가 있어서 단순히 개념을 읽고 넘기는 게 아니라, 직접 문제를 풀면서 이해도를 점검할 수 있다. 배운 내용을 한 번 더 복습할 수 있어서 기억에 오래 남는다는 점이 장점이었다.

5) 코딩 테스트에서 자주 나오는 유형을 다룸

책에서 다루는 개념들이 실제 코딩 테스트에서 자주 등장하는 알고리즘과 문제 유형이 많다. 예를 들어, 이진 탐색, 정렬, 그래프 탐색(BFS, DFS), 재귀, 다익스트라 알고리즘, 동적 프로그래밍(DP), 탐욕 알고리즘 같은 것들이다. 코딩 테스트를 준비하는 사람이라면 기본 개념을 익히기에 좋은 책이다.

6) 개념을 쉽게 풀어주는 방식

단순한 수식과 공식 암기가 아니라, 직관적으로 개념을 이해할 수 있도록 설명해줘서 처음 접하는 사람도 쉽게 따라갈 수 있었다. 특히, 어려운 개념을 친절하게 설명하는 방식이 인상적이었다.

이 책이 특히 추천되는 사람

• 알고리즘을 처음 공부하는 입문자
• 코딩 테스트를 준비하면서 개념을 쉽게 정리하고 싶은 사람
• 이론서보다 직관적으로 개념을 이해하고 싶은 사람
• 두꺼운 알고리즘 책이 부담스러운 사람

책을 더 꼼꼼히 읽어보고 나면 추가로 느낀 점이 있을 것 같은데, 지금까지 본 것만으로도 입문자에게 정말 좋은 알고리즘 책이라고 생각된다. 

알고리즘을 공부해야 하는 이유

알고리즘을 공부하는 이유는 단순히 코딩 테스트를 통과하기 위해서가 아니라, 문제를 해결하는 사고방식을 기르고, 더 효율적인 코드 작성을 할 수 있도록 돕기 때문이다.

특히 이직/취업 관점과 공부 관점에서 각각 중요한 이유가 있다

그러한 이유로 그로킹 알고리즘 책은 입문하기 쉬운 책인 것 같다. 그렇기에 나도 이 책을 기간을 두고 좀 더 깊게 읽을 예정이다. 

이 책은 아마존에서도 높은 평가를 받고 있으며, 전 세계적으로 알고리즘 입문서의 베스트셀러로 자리 잡았습니다. 10만명이 이 책을 봤고, 알고리즘의 개념을 쉽게 이해할 수 있도록 구성된 것이 특징이기도 합니다. 수학적 지식 없이도 알고리즘에 대해 쉽게 이해하고 학습할 수 있습니다. 이는 프로그래밍을 처음 접하는 사람들도 부담 없이 알고리즘의 세계에 입문할 수 있게 해주는 큰 장점입니다. 특히 이번 개정판에서는 트리와 NP-완전 문제에 대한 더 자세한 설명이 추가되어 실무에서도 유용하게 활용할 수 있습니다.

한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다.

그로킹 알고리즘(개정판)은 단순한 이론에 대한 설명이 아니라 직관적으로 체득할 수 있도록 돕는 책입니다. 이 책은 복잡한 개념을 쉽게 풀어내며, 특히 알고리즘을 처음 접하거나 코딩 테스트를 준비하는 사람들에게 좋은 가이드가 됩니다. 

장점 1️⃣. 체계적인 구성

• 시간 복잡도, 빅오 표기법과 같은 기본적인 개념부터 시작해 점진적으로 난이도를 높이는 방식으로 구성되어 있습니다.
• 그래서 초보자도 부담 없이 따라가실 수 있고, 자연스럽게 자료구조와 알고리즘에 대한 이해도를 쌓으실 수 있습니다.
  
  • HashTable과 충돌
  • Array와 LinkedList 비교
• 또한, 각 챕터의 마지막에는 핵심 정리와 연습문제가 포함되어 있어 배운 내용을 복습할 수 있도록 도와줍니다.

장점 2️⃣. 코딩 테스트에서 자주 나오는 유형을 다룹니다

• 이진 탐색, 재귀, 정렬, 그래프 탐색 등 실제 코딩 테스트에서 자주 등장하는 알고리즘을 다루고 있어 실용성이 높습니다.
• 저는 특히 재귀에 대한 이해도를 쌓고 싶어서 이 책을 읽었는데, 완전탐색, 백트래킹, 동적 프로그래밍, 깊이 우선 탐색(DFS) 등 여러 중요한 알고리즘의 기초가 되기 때문에 많은 도움이 되었습니다.
• 단, 파이썬으로된 간단한 예제 코드를 다루므로 기본 문법을 이해하고 읽으시는 것을 권장합니다

장점 3️⃣. 예제와 그림을 통한 직관적 설명

• 텍스트만 있는 이론서와 달리, 이 책은 현실적인 예시와 그림과 함께 개념을 설명하기 때문에 시각적으로 이해하기 쉽습니다.
• 알고리즘이 어떻게 동작하는지 흐름을 따라가다 보면 자연스럽게 개념이 정리됩니다.
• 참고로, 그래프 탐색에서 간선의 가중치에 따라 알고리즘을 선택하는 방법도 명확히 이해할 수 있습니다.
  • 가중치가 1보다 크다면 → 다익스트라 알고리즘 사용 (최소 힙 / 우선순위 큐 활용
  • 가중치가 1이거나 일정하다면 → BFS(너비 우선 탐색) 사용 (큐 활용)
  • 가중치가 음수이고 순환이 발생한다면 → 벨만-포드 알고리즘 사용

❗ 이 책을 읽는다고 해서 바로 코딩 테스트 문제를 풀 수 있는 것은 아닙니다.

• 즉, 알고리즘을 이해하는 데 초점이 맞춰져 있어 실전 문제 풀이는 따로 연습이 필요합니다.
• 하지만, 개념을 탄탄히 다지고 새로운 인사이트를 얻는데는 큰 도움이 됩니다.

그림으로 개념을 이해하는 "그로킹 알고리즘" - 한빛미디어

그로킹(Grokking)"이라는 단어는 "완전히 이해하다" 또는 "깊이 있게 이해하다"는 뜻으로 사용됩니다. 이 단어는 미국의 작가 로버트 A. 하인라인의 소설 Stranger in a Strange Land에서 처음 등장했으며, 그 이후로 기술적이거나 복잡한 개념을 완전히 이해하는 상태를 표현하는 데 사용됩니다. 따라서 "그로킹 알고리즘"은 알고리즘을 단순히 외우는 것이 아니라, 그 동작 원리와 효율성 등을 깊이 이해하고, 실제로 어떻게 사용되는지까지 완전히 파악하는 것을 목표로 한다는 의미입니다.

책을 펼치는 순간, 학부시절에 들었던 자료구조, 컴퓨터구조, 알고리즘 수업이 생각났다. 이 책을 그때 접했다면 “더 쉽게 개념을 이해했을텐데”라는 생각이 들 정도로 실생활에 비유한 그림으로 이해를 가속화 시키는 기분을 들게 해주더라.

단순 탐색과 정렬은 너무나 오랜 시간이 걸린다. 보다 더 효율적인 알고리즘을 통해 시간과 성능을 높이고 효율화하면 우리의 소중한 시간을 더욱 아낄 수 있고 더 좋은 결과물을 만들어낼 수 있다.

이진탐색, 정렬, 스택, 해시, 다익스트라, 그래프, 병렬 알고리즘, 맵리듀스 등 기본적인 알고리즘부터 시작해서 추가로 익혀야될 부분을 책에서는 고루고루 이야기해주고 있다. 이해하기 쉽게 그림으로 설명하고 거기에 덧붙여 파이썬 코드를 통해 실제로 따라해보면서 라인별로 이해할 수 있게 설명까지 되어있다. 마지막으로 챕터별 연습문제까지 독자에게 제공해주고 있다.

빅오 표기법에 대한 기본 개념과 여러 설명이 인상 깊었다. (역시 글보다는 그림으로 이해하는게 최고..!)

다른 개념들도 실생활에서 쓰는 방식으로 설명해주어서 이해하기 쉬웠고, 어려운 포인터는 개념적으로 이해하도록 팁으로 소개하고 있었다.

무슨 알고리즘이 어떤 방식으로 동작하는지 그리고 왜 필요하고 어떻게 사용되는지에 대한 설명이 있어서 이해하기가 쉽고 재밌게 다가온다.



책을 추천하는 이유

이 책은 알고리즘을 배우는 데 있어 그림과 비유를 활용하여 이해도를 높여주는 점에서 다른 알고리즘 서적들과 차별화됩니다. 기본적인 알고리즘부터 시작하여 현업에서 필요한 추가 개념까지 고루 다루고 있어, 현업 개발자에게도 유익한 책입니다. 또한, 실제 개발에 적용하면서 축적된 경험을 통해 더 깊이 있는 이해가 가능하므로, 실용적인 학습이 이루어집니다. 알고리즘을 처음 배우거나 더 깊게 공부하고자 하는 분들에게 이 책을 강력히 추천합니다.

"한빛미디어 서평단 <나는리뷰어다> 활동을 위해서 책을 협찬 받아 작성된 서평입니다."



본 포스팅은 한빛미디어 <나는 리뷰어다> 활동을 위해서 책을 제공받아 작성된 서평입니다. ​

이 책은 독자가 알고리즘의 복잡한 개념에 직면했을 때

느낄 수 있는 혼란과 두려움을 최소화하기 위해,

​

복잡한 알고리즘 개념을 직관적이고

이해하기 쉬운 방식으로 풀어내어,

​

독자가 자연스럽게 알고리즘의 원리를

체득할 수 있도록 돕는다.

​

실제로 책 전반에 걸쳐 등장하는 400개 이상의

일러스트와 생생한 예제들은 독자가 눈으로 보고,

​

직접 문제 해결 과정을 따라가며

이해할 수 있도록 설계되어 있다.

​

각 알고리즘의 작동 원리와 응용 사례는

추상적인 이론보다는 구체적인 상황과

연결되어 설명되기 때문에,

​

독자는 마치 실제 문제를 해결하는

현장에 있는 듯한 생동감을 느낄 수 있다.

​

예를 들어, 이진 탐색과 재귀 개념은

단순한 코드의 흐름을 넘어서,

실생활의 다양한 상황에 비유되어 설명되므로,

복잡한 알고리즘 원리가 단번에 머리에 쏙 들어온다.

​

뿐만 아니라, 삽화와 도표, 그리고 다양한 예시 코드들은

독자가 이해의 단계를 하나하나 밟아 나갈 수 있도록 돕는다.

업계 전문가들의 극찬과 추천이 이어지는

'그로킹 알고리즘(개정판)'은,

단순히 알고리즘의 기초를 다루는 입문서를 넘어,

실무에서의 응용과 심화 학습까지

아우르는 완벽한 안내서로 평가받고 있다.

​

업계 전문가들의 극찬과 추천사는

이 책이 단순한 입문서를 넘어,

​

알고리즘의 깊은 이해와 실무 적용 능력을

키워주는 최고의 안내서임을 입증한다.

​

케이티 사일러 밀러, 벤 비니거, 알렉산더 매닝 등

유명 전문가들이 이 책을 추천한 이유는 명료한 설명과

풍부한 시각 자료, 그리고 단계별 학습 시스템에 있다.

​

이들은 책의 체계적인 구성과 실용적인 예제,

그리고 실제 문제 해결에 초점을 맞춘 접근법이

독자들에게 단순한 지식 전달을 넘어서,

실전에서 바로 활용 가능한 능력을 길러준다고 극찬한다.

​

전문가들은 특히 복잡한 알고리즘 개념을 쉽게 풀어내어,

초보자와 경험자 모두가 공감할 수 있는

설명 방식에 주목하며, 이러한 접근법이

앞으로의 IT 산업에서 필수적인 문제 해결 능력을

배양하는 데 큰 역할을 할 것이라고 평가한다.

​

또한, 심도 있는 이론과 실무 적용 사례를

균형 있게 담아낸 점은, 학습자가 단순한 암기를 넘어

실제 업무에서 발생하는 다양한 문제를 창의적으로

해결할 수 있는 기반을 마련해준다.

​

이와 같이, 책은 단순한 기술 서적을 넘어서,

알고리즘 학습 전반에 대한 심층적인 분석과

응용 전략을 제시하며, 독자들이 이론과 실무를

동시에 익힐 수 있도록 돕는다.

​

결과적으로, '그로킹 알고리즘(개정판)'은

알고리즘 학습에 최적화된 완벽한 안내서로서,

현재의 IT 환경에서 경쟁력을 갖추기 원하는

모든 개발자들에게 큰 도움이 되는 필독서임이 분명하다.

​

전문가들의 추천과 함께,

이 책은 앞으로도 꾸준히 사랑받을 만한

가치 있는 자료로 자리매김할 것이다.